 |
Chirurgia spinală minim invazivă
Chirurgia spinală minim invazivă oferă pacienților oportunitatea unui tratament eficient, permițându-le o recuperare ultra rapidă și nu în ultimul rând minimizând leziunile induse chirurgical. Echipa noastră utilizează un spectru larg de tehnici minim invazive, din care enumerăm câteva: endoscopia cu variantele ei (transnazală, transtoracică, transmusculară, etc), microscopul operator, abordurile trans tubulare și nu în ultimul rând infiltrațiile la toate nivelurile coloanei vertebrale. www.neurohope.ro |
Optimizare cu Excel Solver si metoda celor mai mici patrate
#19
 Posted 18 December 2021 - 12:18
Posted 18 December 2021 - 12:18

|
Dacă explici exact ce vrei sa faci, pot sa încerc să-ți dau o idee. Excel are deja solver incorporat, nu-i nevoie să-l faci tu. Nu-i solver pentru cele mai mici pătrate ci unul generic însă îl poți utiliza. Eu de ex l-am folosit pentru regresii. Am curbe măsurate și voiam sa le aproximez cu niște polinomiale (gr3, cu 4 coeficienți deci) . Calculezi suma pătrățelor direct în excel, și apoi folosești solver ul ca să o minimizezi calculând valoarea celor 4 coeficienți ai polinomului. Cum se folosește exact solver ul incorporat e destul de intuitiv, nu prea ai nevoie de prea multe instrucțiuni. In prima faza am o ecuatie care produce o curba target ( curba ideala ) , unde am X si Yideal Si am ( un caz simplu ) trei perechi de : acelasi X la toate , si : Y1real , Y2real , Y3 rea Si combinatia dintre perechile X-Y1real , X-Y2real , X-Y3real va produce o curba , care sa se apropie cat mai mult de curba ideala . X = 16 , 8 , 4 , 2 , 1 , 0.5 , 0.25 , 0.125 ( progresie geometrica ) X e acelasi la in ambele cazuri , si la curba ideala , si la curba reala produsa din cele trei perechi de X-Y1real , X-Y2real , X-Y3real Y-ul ideal e in Excelul atasat la coalana : Y Ideal In imaginea "Curba_Reala ) se pot vedea perechile de : X-Y1real , X-Y2real , X-Y3real === Curba rezultata din combinatia celor trei perechi de : X-Y1real , X-Y2real , X-Y3real trebuie sa fie cat mai apropiata de curba ideala . Attached FilesEdited by luk2011, 18 December 2021 - 12:19. |
#20
 Posted 18 December 2021 - 12:36
Posted 18 December 2021 - 12:36

|
Curba rezultata din combinatia celor trei perechi de : X-Y1real , X-Y2real , X-Y3real trebuie sa fie cat mai apropiata de curba ideala .
In imaginea "Grafic.jpg" se poate vedea despre ce e vorba mai exact . Curba rezultatata din combinatiile curbelor individuale ( X-Y1real , X-Y2real , X-Y3real ) trebuie sa se apropie cat de mult posibil de curba ideala ( curba data de ecuatia din Excelul atasat ) "Target Function" = Curba Ideala "Composed Mix" = combinatia celor trei perechi de : X-Y1real , X-Y2real , X-Y3real Attached FilesEdited by luk2011, 18 December 2021 - 12:38. |
#21
 Posted 18 December 2021 - 12:41
Posted 18 December 2021 - 12:41

|
Deci trebuie sa cauti parametrii q, dm si D (celulele C4, C5, C6) in asa fel incat curba ideala sa fie cat mai apropiata de cea reala? Daca asta e tot a regresie suna.
Baga in tot in fisierul excel si curba (sau Y) reala, nu doar pe cea ideala. Edited by KiloW, 18 December 2021 - 12:41. |
#22
 Posted 18 December 2021 - 12:52
Posted 18 December 2021 - 12:52

|
Deci trebuie sa cauti parametrii q, dm si D (celulele C4, C5, C6) in asa fel incat curba ideala sa fie cat mai apropiata de cea reala? Daca asta e tot a regresie suna. Baga in tot in fisierul excel si curba (sau Y) reala, nu doar pe cea ideala. In imaginea atasata sint perechile de curbe reale : X-Y1real , X-Y2real , X-Y3real Ceea ce ma intereseaza e procentul din X-Y1real , procentul din X-Y2real si procentul din X-Y3real , in asa fel incat suma procentelor din curbelor individuale = 100% , si curba reala rezultata din combinatiile ( mixajul / mestecul ) celor 3 curbe individuale sa fie cat mai apropiata de curba ideala . Attached FilesEdited by luk2011, 18 December 2021 - 13:07. |
#23
 Posted 18 December 2021 - 13:48
Posted 18 December 2021 - 13:48

|
Procentele astea 3 vrei sa le optimizezi?
 Untitled.png 461K
6 downloads
Untitled.png 461K
6 downloads
Edited by dani.user, 18 December 2021 - 13:48. |
#24
 Posted 18 December 2021 - 13:54
Posted 18 December 2021 - 13:54

#25
 Posted 18 December 2021 - 15:19
Posted 18 December 2021 - 15:19

|
Deci trebuie sa cauti parametrii q, dm si D (celulele C4, C5, C6) in asa fel incat curba ideala sa fie cat mai apropiata de cea reala? Daca asta e tot a regresie suna. Baga in tot in fisierul excel si curba (sau Y) reala, nu doar pe cea ideala. q = 0.21 - 0.37 , pentru beton normal q = 0.37 pentru beton autocompactant q = 0.21 - 0.25 ( de ex : 0.23 ) dar pentru beton normal : q = 0.37 Dmax = 16mm Dmin = 0.125mm Curba reala compusa din mixajul celor trei sorturi : 0 - 4mm , 4 - 8mm si 8 - 16mm , trebuie sa fie cat mai apropiata de curba ideala ( exprimata de ecuatia din Excel ) Prin minimizarea RSS ( residual sume of squares - metoda celor mai mici patrate ) se obtine cea mai apropiata curba de aceea ideala . Ceea ce caut ii : procentele celor trei sorturi : cat la % trebuie sa folosesc din sortul : 0 - 4mm cat la % trebuie sa folosesc din sortul 4 - 8mm cat la % trebuie sa folosesc din sortul 8 - 16mm Edited by luk2011, 18 December 2021 - 15:21. |
#26
 Posted 18 December 2021 - 17:41
Posted 18 December 2021 - 17:41

|
Vin cu o erata, am gresit niste chestii sau am introdus niste confuzii.
. Cred ca am incurcat topicurile, nu mai stiu unde am postat originalul, dar nu conteaza, asta-i varianta corectata. Attached Files |
#27
 Posted 18 December 2021 - 18:27
Posted 18 December 2021 - 18:27

|
@dani.user te stii in Matlab ?
Ca am codul sursa la un program din asta de optimizare a distributiei de particule facut in Matlab . programul Matlab e conectat la un tabel Excel . |
#28
 Posted 18 December 2021 - 19:27
Posted 18 December 2021 - 19:27

|
Cateva aspecte care fac diferenta intre matematica si inginerie.
Pe scurt, matematica e buna, atunci cand e buna. Cand e rea, nu mai e buna. Vorba lu Hagi. La fel si calculele inginieresti. Cand bagi valori "ortodoxe", asteapta-te la valori ortodoxe. Cand bagi valori sataniste, asteapta-te la rezultate sataniste. Sau, matematica si inginieria nu sunt compatibile in toate cazurile. De aia una trebuie sa vina in intampinarea alteia. Uite un exemplu, cand inginieria vine in intampinarea matematicii. Sa zicem ca ai doua sorturi de agregate absolut identice. Well, in cazul asta, nu te astepta la un rezultat unic, pentru ca procentul dintre cele doua sorturi nu mai conteaza in acest caz. Matematica nu vrea probleme cu solutii nonunice. Asadar, ceva va crapa acolo. In acest caz, va crapa inversarea matricei A'A, deoarece va avea det zero. Asta-i un caz banal, dar se poate ca un sort sa fie media perfecta intre alte doua sorturi, caz in care iarasi, ai o solutie nonunica, de data asta nu in mod evident vizibila. Ca atare, nu o vei putea evita, iar matematica va crapa. Va trebui sa vezi motivul pentru care acest lucru se intampla. Sau, poate ca determinantul nu da fix 0, dar aproape, caz in care vei avea instabilitate numerica, cu valori absurde. Apoi, suma aia a patratelor minime, e oleaca cu skepsis. De exemplu, daca toate sorturile produc 0% pe sita 1, iar rezultatul final vrei sa aiba pe sita 1 un 50%, e clar ca nu e posibil. Asadar, in suma patratelor vei regasi un termen foarte mare. Fiind ridicat si la patrat, asta face ca ceilalti termeni sa fie foarte mici comparativ cu acesta, si foarte sensibili la o mica modificare a procentului de 0% de pe sita unul pe un anume sort. De ce se intampla asta? Well.. e oleaca mai delicat raspunsul, dar suma patratelor unor abateri are sens doar atunci cand abaterile au o distributie normala, sau aproape normala. Sau abaterile pot trece testul de normalitate, care e si el un test statistic, cu parametri in plus. Cand gasesti abateri care, aposterioric, dupa aplicarea aparatului matematic, vezi ca nu sunt normale, adica in cazul expus de tine, sita 1 si sita 2 ies afara din "schema", inginiereste ar fi nevoie sa reconsideri metoda celor mai mici patrate si sa o transformi intr-o metoda sumei ponderate a celor mai mici patrate, in care sa acorzi o "importanta" mai slaba a valorilor iesite din "normal" si sa refaci calculul. Matematic nu va mai fi un rezultat bazat pe least-squares, dar va fi un rezultat mai corect din pdv inginieresc. Ca atare, metoda trebuie "tunata" si posibil ca in manualele de agregate exista o astfel de metoda, "tunata" Venind acum din cealalta parte, dinspre matematica inspre inginierie, putem relaxa oleaca metoda, introducand ponderi abaterilor. Mai precis. Ai cate o ecuatie pentru fiecare sita si cate o necunoscuta pentru fiecare (fara ultimul) sort de agregate. Matematic, e usor sa modifici metoda pentru a permite introducerea ponderilor asupra fiecarei ecuatii, adica asupra importantei fiecarei site. Daca punem ponderile sub forma unei matrici diagonala P, unde Pii= nonzero si Pij=0, pentru i diferit de j., aparatul matematic se transforma astfel: Conditia 1 V=AX+T ramane. Conditia 2 V'V=minim devine V'PV=minim Rezultatul X va fi: X=(A'PA)-1A'PT iar la estimarile de eroare, vei avea sigma, un scalar reprezentand eroarea unei abateri cu pondere 1, denumit "eroarea medie patratica a unitatii de pondere" sigma0= V'PV / (n-m+1) unde n= numarul de site, m numarul de sorturi. iar velorile sigmaVV, ale variantei abaterilor se calculeaza sigmaVV=sigma0*P. Formula pentru sigmaXX ramane aceiasi Formula pentru sigmaFF ramane aceiasi. Bun! Acum, de unde luam ponderea P pentru fiecare abatere de la model, V? Pentru asta, trebuie sa intram oleaca in filozofia statisticii si a cunoasterii in sens Bayesian a problemei abstracte. La modul concret, ele pot fi implementate in fiecare situatie practica, dar exista si o perspectiva abstracta, comuna tuturor pentru alegerea acestor ponderi si asta se afla in ideea de "update" a cunoasterii in sens Bayesian. Adica.. daca aprioric stii ca V-urile trebuie sa fie distribuite normal, nu intervii si alegi P=1, adica ignori complet ponderie. Asta e cazul pe care ti l=am pus in excel. Si ti-am aratat cum se modifica, daca stii P. Daca insa V-urile vezi aposterioric ca nu au nicio treaba cu distributia normala, insamna ca ai bagat "garbage in" si asteapta-te la ":garbage out" Matematica e toleranta si la aceste aspecte, iar revenind la filozofia de "update in sens Bayesian", transformi problema intr-una de "update a cunoasterii". Adica, faci asa: 1. rezolvi problema plecand de la ipoteza distribuirii normale, obtii un V distribuit departe de normal (masura acestui lucru presupune cunoasterea unor alte concepte, testul Fischer, distributii altele decat normale, chisquare, de exemplu, si alte semnificatii, dar nu ne bagam in zona asta ca-i reteta de beton, nu de medicament. 2. Cu valorile V-urile calculate la pasul 1, calculezi matricea P, unde Pii=1/Vi2, adica setezi ponderea ca fiind inversa patratului abaterii de la punctul 1. 3. Aplici metoda updatata cu Pul calculat la 2. Rezultatul final va capata semnificatia de "cele mai mici patrate relevante", in loc de "cele mai mici patrate". Asta deoarece in inginierie, te intereseaza si cat de relevanta e chestiunea, De exemplu cat de relevanta e sita 1, dat fiind faptul ca niciun sort de agregate nu trece prin ea. E "natural" sa consideri ca nu-i relevanta si e firesc sa nu lasi rezultatul sa fie influentat in aceiasi masura ca celelalte site. In sens filozofic, ai plecat de la o distributie normala, ai vazut ca nu se justifica acest lucru si ai revenit la o metoda adaptata pe distributia nou observata, aposterioric. De unde atata filozofie? Pentru ca trebuie bagare de seama. Cand datele sunt "cat de cat" normale, nu trebuie sa aplici acest artificiu deoarece schimba ipoteza si semnificatia rezultatului. Semnificatia conteaza. E un compromis, iar masura care sta la baza acestui compromis o reprezinta testul statistic, inferenta statistica asupra ipotezei de normalitate, chestiune oleaca diferita de problema in cauza, nu neaparat dificil de inteles, dar din fericire e usor de aplicat prin "manipularea" ponderilor inspre 1/V2 .Matematica e agnostica la inginierie si invers. Ele trebuiesc aduse "in impedanta" sa poata lucra. Fie cu un shift de paradigma atat dintr-o parte cat si din alta. Mai renunti la ecuatii ( sorturi ), daca vezi ca rezultatul nu e unic (matricea e neinversabila sau inversarea e instabila numeric) Matematica te ajuta sa-ti dai seama care-i problema, dar problema trebuie corectata dinspre partea de inginierie. La fel, daca matematica "lucreaza" perfect, insa da rezultate neasteptate (in sens Bayesian, adica abatere de la normalitate), atunci ajustam matematica, facem un shift de paradigma in ceea ce priveste semnificatia purtata de noile variabile implicate si rezolvam "inginiereste" problema. Trebuie spus ca se poate rezolva si "perfect" matematic, insa cu lanturi Markov si alte tampenii foarte greu de inteles si pus in opera, cu rezultate "apropiate" de varianta "ajustata". Cred ca-i bun adaosul asta de cuvinte, sa nu facem calcule in care nu credem, de dragul matematicii, sau calcule gresite de dragul inginieriei. Ce facem e o modelare a realitatii, nu reprezentarea fidela a realitatii. Par vrajeli, dar sunt importante chestiile astea, altfel nu ai cum sa faci lucrurile sa mearga si nu poti controla semnificatia calculelor, rezultatelor. Cateodata esti pe realitate, altatata pe model, trebuie sa ai harta sa nu te ratacesti si sa confunzi chestii pe-acolo. Edited by maccip, 18 December 2021 - 19:29. |
|
#29
 Posted 18 December 2021 - 21:05
Posted 18 December 2021 - 21:05

|
Am reusit sa fac Excelul sa functioneze Cu Solverul reusesc sa minimizez RSS-ul ( residual sume of squares - metoda celor mai mici patrate ) si sa obtin procentele din fiecare sort in asa fel incat sa ma apropiu cat de mult posibil de : Target Function , adica de curba ideala ( curba ecuatiei lui Funk&Dinger - sau altfel spus ecuatiei modificate a lui Andreasen ) Se poate vedea in imaginea atasata . Orinea de introducere a datelor este numerotata pe imaginea atasata de la 1. pana la afisarea graficului 7. Ramane sa reusesc cumva sa adaug si R^2 - coeficientul de determinatie , in asa fel incat R^2 sa tinda spre valoarea = 1 . Ecuatia lui R^2 - coeficientul de determinatie se poate vedea in imaginea atasata . Quote As a criterion for the evaluation of the quality of the curve fit, the coefficient of determination R2 according to Eq. (5) is used. This value expresses the proportion of fluctuation between the target line and the obtained values for the grading of the composed mixture and is defined as: ==== Prin optimizarea distributiei de particule avand ca Functia Target ( curba ideala ) ecuatia Funk&Dinger am obtinut procentele din imaginea atasata , adica : sort : 0 -4mm = 55.5 % sort : 4- 8mm = 22.9 % sort : 8 -16mm = 21.6 % Attached FilesEdited by luk2011, 18 December 2021 - 21:14. |
#30
 Posted 18 December 2021 - 21:34
Posted 18 December 2021 - 21:34

|
Target Function = Funk&Dinger ( sau modified Andreassen ) - se poate vedea in imaginea atasata , a doua ecuatie .
Coefficient of determination https://en.wikipedia...f_determination Quote
„For “normal concrete”, most design codes require continuous grading to achieve tight packing. Continuous grading curves range from 250μm to a maximum particle size and are S-shaped in a single-logarithmic graph (Fuller curve). For modern concretes, such as High Strength Concrete and SCC this Fuller curve is less suited. This curve is applicable to materials with a particle size larger than 500μm. Applying this grading curve to materials with fine constituents results in mixes that are poor in cement and that are less workable. Standards therefore require a minimum content of fine materials (< 250μm) in normal concrete. As the content and PSD of fine materials (powder) cannot be determined properly with the Fuller curve, it is less suited for SCC as a large part of the solids consist of powder. Actually, the packing theory of Fuller and Thompson represents a special case within the more general packing equations derived by Andreasen and Andersen [4]. According to their theory, optimum packing can be achieved when the cumulative PSD obeys the following equation:“ „The figure confirms that the grading curve of A&A better accounts for powders than the grading curve of Fuller. From the curves in Figure 2 it furthermore follows that about 20% of the particles are finer than 75μm, whereas, according to Fuller, only 5.5% are smaller than 75μm. As the A&A model accounts for powders (< 250μm) better, it is better suited for designing SCC. A continuous grading of all solids (aggregate and powders) will result in a better workability and stability of the concrete mix.“ https://josbrouwers....onference15.pdf Attached FilesEdited by luk2011, 18 December 2021 - 21:45. |
#31
 Posted 18 December 2021 - 21:46
Posted 18 December 2021 - 21:46

|
Valorile calculate de tine sunt corecte.
Am facut eu niste verificari si am gresit la inmultirea matricelor A'M (daca verifici in excelul vechi, matricea A' are referinta aiurea). Am corectat eroarea si acum imi da si mie la fel ca tine. Asta inseamna ca suntem convergenti pana la urma. Attached Files |
#32
 Posted 18 December 2021 - 22:04
Posted 18 December 2021 - 22:04

|
De fapt mai e o greseala la calculul lui SigmaV,, daca ti-o trebui la ceva. Formula initiala e gresita, cea corecta e aici.
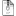 Amestec agregate.zip 15.48K
0 downloads
Amestec agregate.zip 15.48K
0 downloads
|
#33
 Posted 18 December 2021 - 22:14
Posted 18 December 2021 - 22:14

|
Mersi mult @maccip .
Am verificat rezultatul prin mai multe metode , si eu asa cred ca la datele ecuatiei trecute pe imaginea de mai sus , rezultatul e corect . Mai ramane sa implementez cumva R^2 coeficientul de determinatie . Chestia asta nu tine doar de beton . Ci e vorba de : Distributie de Particule ( Packing Density ) Se aplica in foarte multe domenii : si in ceramica ( eu asa stiu ) , si in alte domenii unde distributia compacta a particulelor e foarte importanta . Edited by luk2011, 18 December 2021 - 22:18. |
|
#34
 Posted 18 December 2021 - 22:30
Posted 18 December 2021 - 22:30

|
Si inca o greseala, la naiba. La calculul SigmaXX (trebuia inmultit cu patratul lui SigmaV, nu doar cu SigmaV)
Am facut si SigmaFF, daca vrei sa vezi si abaterea standard a procentelor calculate, inclusiv pentru ultimul sort dependent de celelalte. Nu stiu daca-ti foloseste, insa e bine sa fie corect. Mai bine faceam in Google Sheets si corectam pe parcurs fara sa mai tot fac upload. Sau si mai bine, verificam rezultatul de la bun inceput. Aia e! 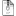 Amestec agregate.zip 15.28K
1 downloads
Amestec agregate.zip 15.28K
1 downloads
|
#35
 Posted 18 December 2021 - 22:32
Posted 18 December 2021 - 22:32

|
Si inca o greseala, la naiba. La calculul SigmaXX (trebuia inmultit cu patratul lui SigmaV, nu doar cu SigmaV) Am facut si SigmaFF, daca vrei sa vezi si abaterea standard a procentelor calculate, inclusiv pentru ultimul sort dependent de celelalte. Nu stiu daca-ti foloseste, insa e bine sa fie corect. Mai bine faceam in Google Sheets si corectam pe parcurs fara sa mai tot fac upload. Sau si mai bine, verificam rezultatul de la bun inceput. Aia e! Nu e nici o problema . Doar cine nu incearca , nu greseste |
#36
 Posted 18 December 2021 - 22:33
Posted 18 December 2021 - 22:33

|
Mai ramane sa implementez cumva R^2 coeficientul de determinatie . Se calculeaza cumva? N-as sta sa ling toate documentele pe care mi l-ei trimis. Ce reprezinta, la ce se foloseste si cum se calculeaza? Nu vad unde ar intra aici, poate doar in calculul valorilor model, dar acolo vad ca ai o formula (simpla). |
Anunturi
▶ 0 user(s) are reading this topic
0 members, 0 guests, 0 anonymous users
 Sign In
Sign In Create Account
Create Account



 Back to top
Back to top
